티스토리 뷰
1. 집합 A의 관계 R에 대하여 다음 물음에 답하시오.
A = { 1,2,3,4 }
R = { (1,1), (1,2). (2,1), (2,2), (2,3), (3,2), (3,4), (4,1), (4,2), (4,4) }
(1) 관계 R을 방향 그래프로 나타내시오
- 관계 R을 방향 그래프로 나타내면 아래와 같이 나타낼 수 있다.
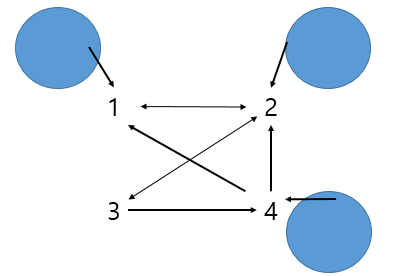
(2) 관계 R을 부울행렬로 나타내시오
- 관계 R을 방향 부울행렬로 나타내면 아래와 같이 나타낼 수 있다.
- 집합 A의 관계 R을 부울행렬로 나타낸 것을 A라고 하자,

(3) 관계 R이 반사적인지 밝히시오
- 집합A의 관계 R이 반사적이 되려면 ∀x∈A에 대하여 (x,x)∈R이어야한다. 그러나 집합 A의 원소들 중 3에 대해서는 (3,3)∉A이기 때문에 관계 R은 반사적이지 않다.
(4) 관계 R이 대칭적인지 밝히시오
- 집합 A의 관계 R이 대칭적이 되려면 ∀x,y∈A에 대해 (x,y)∈R일 때, (y,x)∈R을 만족해야한다. 그러나 (3,4)∈R이고 (4,3)∉R이기 때문에 관계 R은 대칭적이지 않다.
(5) 관계 R이 추이적인지 밝히시오
- 집합 A의 관계 R이 추이적이 되려면 x,y,z∈A에 대해 (x,y)∈R & (y,z)∈R일 때, (x,z)∈R을 만족해야 한다. 그러나 (1,2)∈R & (2,3)∈R이고 (1,3)∉R이므로, 관계 R은 추이적이지 않다.
2. 그래프에 관한 다음 물음에 답하시오.
(1) K6 의 그래프를 그리시오

(2) K6 의 그래프를 인접행렬로 나타내시오
- K6 의 인접행렬을 A행렬이라고 하자,
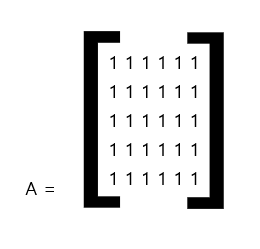
(3) K3,5 의 그래프를 그리시오

(4) K4,3 의 총 차수를 구하시오.
- 그래프의 총 차수는 24이다. (4 X 3 + 3 X 4)

3. 다음 그래프에 관하여 물음에 답하시오.

(1) 오일러 투어가 있는지 확인하고, 있다면 구하시오.
- 위의 그래프를 G = (K, E) 라고 정의(K를 해당 그래프의 꼭지점들의 집합이라고 정의)를 했을 때 오일러투어의 정의에 의해서 그래프가 오일러 투어를 가진다면 그 그래프의 모든 꼭지점의 차수는 짝수라고 할 수 있다. 그런데 그래프의 꼭지점들의 집합인 K의 원소 중 { b, e, f, g }의 차수는 홀수 이므로 그래프 G는 오일러 투어를 가지지 않는다고 할 수 있다.
(2) 해밀턴 사이클이 있는지 확인하고, 있다면 구하시오
- 위 그래프의 해밀턴 사이클은 꼭지점을 a → b → d → f → z → c → e → g → a 의 순서로 지나가는 경로이다.
(3) 데이크스트라 알고리즘을 이용하여 꼭지점 a에서 꼭지점 z까지의 최단경로를 구하시오
- 데이크스트라 알고리즘을 통하여 얻은 a에서 z까지의 최단거리는 18이다.
- C언어로 구현한 데이크스트라 알고리즘
#include <stdio.h>
#include <limits.h>
// 정점의 수는 8로 정함
#define VERTEX 8
// 하나의 정점인 시작점에서 다른 한 정점까지의 거리 출력하는 함수
void printDistanceFromSource(int distance[], int n)
{
printf("Print Distance\n");
for (int i = 0; i < VERTEX; i++)
printf("%d \t\t %d\n", i, distance[i]);
}
int getMinimumDistance(int distance[VERTEX], bool status[VERTEX])
{
int min = INT_MAX, min_index;
for (int v = 0; v < VERTEX; v++)
{
if (!status[v] && min > distance[v])
{
min_index = v;
min = distance[v];
}
}
return min_index;
}
//데이크스트라 알고리즘을 실행하는 함수
void dijkstra(int graph[VERTEXVERTEXV], int src)
{
int distance[VERTEX];
bool status[VERTEX]; //해당 꼭지점을 지나갔는지 여부를 저장하는 배열
for (int i = 0; i<VERTEX; i++)
distance[i] = INT_MAX, status[i] = false;
distance[src] = 0;
for (int count = 0; count < VERTEX - 1; count++)
{
int u = getMinimumDistance(distance, status);
for (int v = 0; v < VERTEX; v++)
{
if (!status[v] && graph[u][v] && distance[u] != INT_MAX && distance[v]> distance[u] + graph[u][v])
{
distance[v] = distance[u] + graph[u][v];
}
}
status[u] = true;
// 현재까지의 최단거리 출력
printDistanceFromSource(distance, VERTEX);
}
}
int main()
{
//그래프 데이터 정의
int graph[VERTEX][VERTEX] =
{
{ 0, 4, 3, 99999, 99999, 99999, 99999, 99999 },
{ 4, 0, 2, 5, 99999, 99999, 99999, 99999 },
{ 3, 2, 0, 3, 6, 99999, 99999, 99999 },
{ 99999, 5, 3, 0, 1, 5, 99999, 99999 },
{ 99999, 99999, 6, 1, 0, 99999, 5, 99999 },
{ 99999, 99999, 99999, 5, 99999, 0, 2, 7 },
{ 99999, 99999, 99999, 99999, 5, 2, 0, 4 },
{ 99999, 99999, 99999, 99999, 99999, 7, 4, 0 }
};
dijkstra(graph, 0);
return 0;
}- Total
- Today
- Yesterday
- 일본 자전거 여행
- git
- 텐트
- TableView
- java
- 일본 배낭여행
- 일본 여행
- 이펙티브 자바
- 일본여행
- 배낭여행
- 인텔리제이
- intelij
- 자전거 여행
- 자바
- 방통대 과제물
- effectivejava
- JavaFX 종료
- windows
- 이펙티브자바
- 이펙티브
- 스프링부트
- JavaFX Table View
- 자전거
- JavaFX
- 배낭 여행
- effective java
- JavaFX 테이블뷰
- JavaFX Window Close
- springboot
- Java UI
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
